563. Simple equation
Peter found in a book a
simple mathematical equation: a*x + b*y = 1.
His interest is only
integral solutions of this equation, and only those for which x ≥ 0. Help Peter to find them.
Input. First line contains the
number of test cases t (0 <
t < 21). Each of the next t lines contains two integers a and b (0 ≤ a, b
≤ 231).
Output. For each test case print in
a separate line one solution: the smallest possible non-negative value of x and corresponding integer value of y. In case if there is no solution,
print “No Solution”.
|
Sample input |
Sample output |
|
3 77 51 10 44 34 79 |
2 -3 No
Solution 7 -3 |
SOLUTION
Extended Euclidean algorithm
Algorithm analysis
Given the values of a and b, using the extended Euclidean algorithm, we find d = GCD(a, b),
x0 and y0 such
that a*x0 + b*y0 = d. Since the equation a*x + b*y = 1 is being solved,
there is no solution for d > 1.
Theorem. All
solutions of the Diophantine equation a*x + b*y = 1 are given with the formula
,
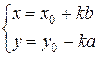where (x0, y0) is a partial solution of the original equation, k Î Z.
Substitute
the pair (x0 + kb, y0 – ka) into the equation a*x + b*y = 1:
a*(x0 + kb) + b*( y0 – ka) = 1,
ax0 + akb + by0 – bka = 1,
ax0 + by0 = 1, ÷òî âåðíî
In order for x to be
the smallest possible non-negative value, it is necessary that k be the smallest for which x0 + kb
≥ 0. Or 
. The smallest integer k that satisfies
the last inequality is 
. For this value of k the solution should
be found and printed.
Since the
extended Euclidean algorithm finds a solution (x0, y0) for which the sum |x0|
+ |y0| is minimal, then
for x0 < 0 the desired
solution (with the smallest non-negative value of x) equals to
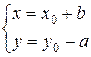
If the
inequality x0 ≥
0 is
satisfied in a partial solution (x0, y0), then it will itself be a
solution to the problem.
Example
Find the partial solution of equation 7x + 11y = 1 with the
smallest possible non-negative value of x. After running
the extended Euclidean algorithm, we get a partial solution x0 = -3, y0 = 2. Really,
7x0 + 11y0 = 7 * (-3) + 11 * 2 = 1
Then 
= 
= 1. The desired
solution to the equation will be
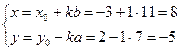
Test: 7 * 8 + 11 * (-5) = 56 –
55 = 1.
Algorithm realization
Function gcdext implements the extended Euclidean algorithm. Given the values of a and b it finds such d, x and y that a*x + b*y = 1.
void gcdext(long long a, long long b, long long &d,
long long &x, long long &y)
{
if (b == 0)
{
d = a; x = 1; y = 0;
return;
}
gcdext(b, a % b, d, x, y);
int s = y;
y = x - (a / b) * y;
x = s;
}
The main part of the program. Read the input data.
scanf("%d",&tests);
while(tests--)
{
scanf("%lld
%lld",&a,&b);
gcdext(a,b,d,x0,y0);
If GCD(a, b) > 1, the solution does not exist.
if (d > 1)
printf("No Solution\n"); else
{
If x0 < 0 in the solution (x0, y0) found by the
extended Euclidean algorithm, then we recalculate it using the formula
indicated in the analysis of the algorithm.
if (x0 <
0) x0 += b, y0 -= a;
printf("%lld
%lld\n",x0,y0);
}
}
Java realization
import java.util.*;
public class Main
{
static long[] GcdExtended(long a, long b)
{
long res[] = new long[3]; // d, x, y
if (b == 0)
{
res[0] = a; res[1] = 1; res[2] = 0;
return res;
}
res = GcdExtended(b,a % b);
long s = res[2];
res[2] = res[1] - (a / b) * res[2];
res[1] = s;
return res;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int tests = con.nextInt();
while(tests-- >
0)
{
long a = con.nextLong(), b = con.nextLong();
long res[] = GcdExtended(a,b);
if (res[0] > 1)
System.out.println("No Solution");
else
{
if (res[1] < 0)
{
res[1] += b; res[2] -= a;
}
System.out.println(res[1] + " " + res[2]);
}
}
con.close();
}
}